Mouse picking can be found in nearly every 3D game now. In many cases, it’s crucial to let the user interact with the world by directly pointing at some objects. One of the possible approaches is to convert pointer position to some vector/ray inside the world and do hit-testing. To achieve this I use GLM library which handles mathematical routines for OpenGL.
Model-View-Perspective Matrices
When we want to render an object, we have to convert its position to OpenGL coordinates, where visible objects are in range [-1, 1]x[-1, 1]x[-1, 1]. You can think of them as some functions. You pass vertices and get the result.
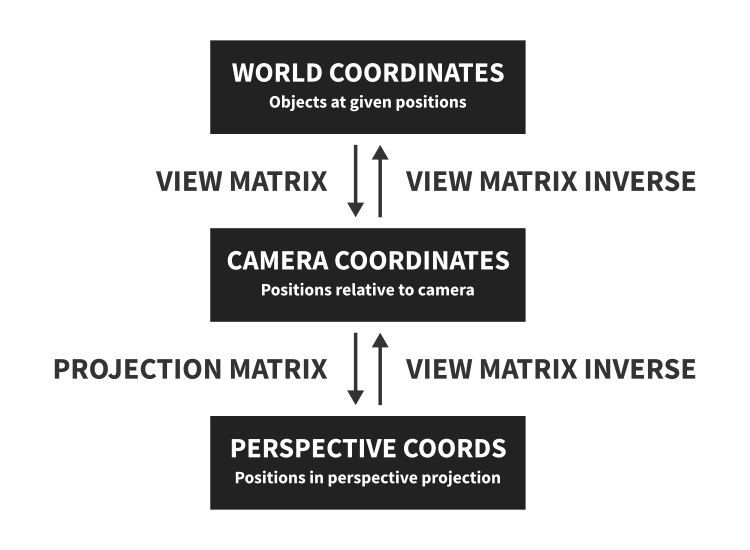
Now, we want to go the other way. We have a 2D vector in perspective coordinates and want to get world coordinates. How to do it?
Linear algebra comes in handy here. We know that world-to-camera and camera-to-perspective transformations can be depicted as vector-matrix multiplication. Also, our matrices are invertible, so we just have to calculate inversions of these functions and we’re done.
Window coordinates
We usually know where the pointer is. For example, we have a window with inner size 800×600. If the mouse is in the middle, it is approximately at point 400×300. Now, OpenGL uses screen coordinates [-1, 1]x[-1, 1] not matter what size is the screen. How to convert between these values?
glm::vec2 viewportSize = glm::vec2(800, 600);
glm::vec2 getMousePositionForRaycasting(glm::vec2 mousePosition) {
return (mousePosition / viewportSize * 2.f) - glm::vec2(1, 1);
}
For example:
getMousePositionForRaycasting(glm::ivec2(400, 300)) == glm::vec2(0, 0) getMousePositionForRaycasting(glm::ivec2(600, 300)) == glm::vec2(0.5, 0) getMousePositionForRaycasting(glm::ivec2(400, 150)) == glm::vec2(0, -0.5) getMousePositionForRaycasting(glm::ivec2(400, 450)) == glm::vec2(0, 0.5)
You should check how your library returns values, in some cases Y axis is inverted.
Getting ray
Let’s assume we have computed projection and view matrices earlier.
// Calculated earlier
glm::mat4 projectionMatrix;
glm::mat4 viewMatrix;
glm::vec3 getRay(glm::vec2 point) {
auto ray = glm::vec4(point.x, point.y, -1.f, 1.0f);
// 1. Projection to view
ray = glm::inverse(projectionMatrix) * ray;
ray = glm::vec4(ray.x, -ray.y, -1.f, 0.0);
// 2. View to world
ray = glm::inverse(viewMatrix) * ray;
ray.w = 0.f;
ray = glm::normalize(ray);
return glm::vec3(ray);
}
1. GetTING A 3D point
We just take our two-dimensional entry point. To make it 3D we add z coordinate (-1 means pointing forwards). We make w coordinate equal 1.
2. Moving from projection to view space
We take projection matrix inverse and multiply. We want out ray to still point forwards in Z axis since it should not be changed by perspective.
3. Moving from view to world space
Now we take view matrix inverse and multiply. The ray which we obtained is in world coordinates. It’s nice to return a normalized vector (i.e. of length equal 1). To do this, we first set w to 0 (to exclude last dimension from computations) and normalize.
Using ray
Now you can use the ray in any way. For example, let’s see how to calculate where ray hits the ground at level y = 0. We need to take our ray and scale it so that its as big (vertically) as high camera is above ground.
const glm::vec3 cameraPosition;
glm::vec3 hitGround(glm::vec2 mousePosition) {
const glm::vec3 ray = getRay(mousePosition);
const glm::vec3 hit = cameraPos - (cameraPosition.y / ray.y) * ray;
return hit;
}
We assume here that your camera rotation does not allow to point above the horizon.
